Una función vista como una «caja negra», que transforma los valores u objetos de «entrada» en los valores u objetos de «salida»
En matemáticas, se dice que una magnitud o cantidad es función de otra si el valor de la primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un círculo es función de su radio r: el valor del área es proporcional alcuadrado del radio, A = π·r2. Del mismo modo, la duración T de un viaje de tren entre dos ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la duración es inversamente proporcional a la velocidad, d / v. A la primera magnitud (el área, la duración) se la denominavariable dependiente, y la cantidad de la que depende (el radio, la velocidad) es lavariable independiente.
| ... | −2 → +4, | −1 → +1, | ±0 → ±0, | |
| | +1 → +1, | +2 → +4, | +3 → +9, | ... |
Esta asignación constituye una función entre el conjunto de los números enteros Z y el conjunto de los números naturales N. Aunque las funciones que manipulan números son las más conocidas, no son el único ejemplo: puede imaginarse una función que a cada palabra del español le asigne su letra inicial:
| ..., | Estación → E, | Museo → M, | Arroyo → A, | Rosa → R, | Avión → A, | ... |
Esta es una función entre el conjunto de las palabras del español y el conjunto de las letras del alfabeto español.
La manera habitual de denotar una función f es:
- f: A → B
- a → f(a),
donde A es el dominio de la función f, su primer conjunto o conjunto de partida; e B es elcodominio de f, su segundo conjunto o conjunto de llegada. Por f(a) se denota la regla oalgoritmo para obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En ocasiones esta expresión es suficiente para especificar la función por completo, infiriendo el dominio y codominio por el contexto. En el ejemplo anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:
- f: Z → N
- k → k2, o sencillamente f(k) = k2;
- g: V → A
- p → Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.
Una función puede representarse de diversas formas: mediante el citado algoritmo o ecuaciones para obtener la imagen de cada elemento, mediante una tabla de valores que empareje cada valor de la variable independiente con su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.
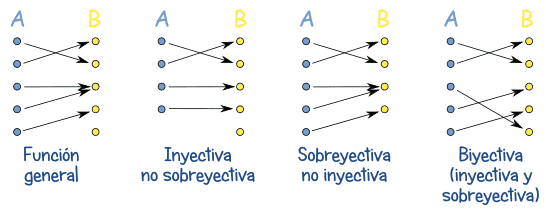
Funciones inyectivas, suprayectivas y biyectivas
La imagen inversa de un elemento del codominio puede ser vacía, o contener varios objetos del dominio. Esto da lugar a la siguiente clasificación:
| Funciones | Inyectiva | No inyectiva |
| Sobreyectiva |
 |
| Biyectiva |
|  |
| No sobreyectiva |  |  |
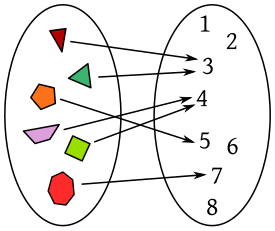
- Se dice que una función f : A → B es inyectiva si las imágenes de elementos distintos son distintas:
- o, de modo equivalente, si sólo asigna imágenes idénticas a elementos idénticos:
- Una función f : A → B se dice suprayectiva (o sobreyectiva) si su imagen es igual a su codominio:
- o, de modo equivalente, si todo elemento del codominio es la imagen de algún elemento del dominio:
|
Las funciones inyectivas no repiten las imágenes: si b = f(a), ningún otro a' tiene por imagen a b, por lo que la anti-imagen de este último sólo contiene al elemento a. Las funciones suprayectivas recorren todo el codominio, por lo que ninguna anti-imagen puede estar vacía. La definición de función suprayectiva asume que esta tiene un codominio especificado previamente. De lo contrario, la noción de suprayectividad no tiene sentido.
Cuando una función tiene ambas propiedades a la vez, se dice que es una biyección entre ambos conjuntos:
Una función f : A → B se dice biyectiva si es inyectiva y suprayectiva.
|
Las funciones biyectivas constituyen un «emparejamiento perfecto» entre los elementos del dominio y el codominio: cada elemento enA tiene una única «pareja» en B —como todas las funciones—, y a cada elemento de B le corresponde uno solo en A —al menos uno por ser suprayectiva, y como mucho uno por ser inyectiva—.
- Ejemplos.
- La función cubo f: R → R es biyectiva. Es inyectiva porque dos números reales que tienen el mismo cubo son idénticos, y es suprayectiva porque Im(f) = R.
- La función «inverso» g: R \ {0} → R es inyectiva, ya que el inverso de cada número real no nulo es único (1/x = 1/y implica necesariamente que x = y). Sin embargo no es suprayectiva, dado que Im(g) = R \ {0}.
- La función de clasificación de mamíferos γ: M → G no es inyectiva, ya que hay mamíferos distintos en el mismo género (por ejemplo, γ(Yak) = γ(Toro) = Bos). Sin embargo sí es suprayectiva, ya que en cada género de mamíferos hay clasificada al menos una especie de mamíferos.
- La función área A: T → R no es sobreyectiva, ya que Im(A) = R+. Tampoco es inyectiva, ya que pueden construirse con facilidad triángulos distintos con el mismo área.
- En la imagen pueden verse varios ejemplos de funciones entre un conjunto de pinceles P y un conjunto de caras C.
Álgebra de funciones
Con las funciones puede realizarse una operación de composición con propiedades similares a las de la multiplicación.
Composición de funciones

La composición g ∘ f actúa sobre el objeto x transformándolo según f, y después transformando f(x) mediante g.
Dadas dos funciones, bajo ciertas condiciones podemos usar los valores de salida de una de ellas como valores de entrada para la otra., creando una nueva función.
Sean dos funciones f : A → B y g : C → D, tales que el recorrido de la primera esté contenido en el dominio de la segunda, Im(f) ⊆C. Entonces puede formarse la composición de g con f, la función g ∘ f : A → D que a cada a en el dominio A le asocia el elemento (g ∘ f)(a) = g(f(a)).
|
Es decir, la composición g ∘ f hace actuar primero la función f sobre un elemento de A, y luego g sobre la imagen que se obtenga:
La condición Im(f) ⊆ C asegura precisamente que este segundo paso se pueda llevar a cabo.
- Ejemplos
- La imagen de la función «inverso» g es R \ {0} —puesto que todo número real no nulo es el inverso de otro—, y por tanto está contenido en el dominio de la función cubo f, que es R. La composición f ∘ g: R \ {0} → R actúa entonces como f(g(x)) = f(1/x) = (1/x)3 = 1/x3.
- Dadas las funciones reales h1: R → R y h2: R → R dadas por h1(x) = x2 y h2(x) = x + 1, puede tomarse la composición en ambos órdenes, h1 ∘ h2 y h2 ∘ h1. Sin embargo, son funciones distintas, ya que:
- (h1 ∘ h2)(x) = h1(h2(x)) = h1(x + 1) = (x + 1)2 = x2 + 2x + 1, y
- (h2 ∘ h1)(x) = h2(h1(x)) = h2(x2) = x2 + 1
- La función γ que clasifica los mamíferos en géneros puede componerse con la función ω: G → Or que clasifica los géneros de mamíferos en órdenes —que forman el conjunto Or—. La función ω ∘ γ asigna a cada mamífero su orden:
- (ω ∘ γ)(Humano) = ω(Homo) = Primate, (ω ∘ γ)(Guanaco) = ω(Lama) = Artiodactyla
Función identidad
En cualquier conjunto puede definirse una función identidad, que teniendo como dominio y codominio al propio conjunto, asocia cada elemento consigo mismo.
Dado un conjunto A, la función identidad de A es la función idA : A → A que a cada a ∈ A le asocia idA(a) = a.
|
También se denota como IA. La función identidad actúa como un elemento neutro al componer funciones, ya que no «hace nada».
Dada una función cualquiera f : A → B se tiene:
|
Es decir, dado un elemento x ∈ A, se tiene que:
Función inversa
Una función puede tener inversa, es decir, otra función que al componerla con ella resulte en la identidad, del mismo modo que un número multiplicado por su inverso da 1.
Dada una función f : A → B, se dice que g : B → A es la inversa o recíprocade f si se cumple:
La inversa se denota por g = f−1, y tanto f como f−1 se dicen invertibles.
|
No todas las funciones son invertibles, sino que solo aquellas que sean biyectivas poseen inversa:
Toda función biyectiva f es invertible, y su inversa f−1 es biyectiva a su vez. Recíprocamente, toda función invertible f es biyectiva.
|
La notación para funciones inversas puede ser confusa. Para un elemento del codominio b, f−1(b) puede denotar tanto la anti-imagen de b (un subconjunto del dominio), como a la imagen de b por la función inversa de f (un elemento del dominio), en el caso de que fsea invertible.
- Ejemplos.
- La función «exponencial» h: R → R, que asocia a cada número real su exponencial, h(x) = ex, no es invertible, ya que no es suprayectiva: ningún número negativo pertenece a la imagen de h.
- Existe una función que calcula el cambio entre dos divisas. En el caso del cambio de rupias a quetzales (las monedas de la Indiay Guatemala), la conversión está dada (en 2011) por:
Q(r) = 0,15 × r
Esta función de cambio tiene inversa, la conversión recíproca de quetzales a rupias:
R(q) = 6,65 × q
- La función cubo f(x) = x3 es invertible, ya que podemos definir la función inversa mediante la raíz cúbica, f−1(x) = 3√x.
- La función de clasificación en géneros γ: M → G no es invertible, ya que no es inyectiva, y para cada género pueden existir varios mamíferos clasificados en él.
- La función que asigna a cada día de la semana su siguiente tiene por inversa la función que asigna a cada día de la semana su antecesor:
- Lunes → Domingo, Martes → Lunes,..., Domingo → Lunes
Restricción y extensión

La función que asigna a cada mujer del electorado su voto es una restricción de la función que a cada miembro del electorado le asigna su voto.
La restricción de una función dada es otra función definida en una parte del dominio de la original, pero que «actúa igual» que esta. Se dice también que la primera es una extensión de la segunda.
Dadas dos funciones f : A → B y g : C → D, de forma que el dominio de g sea un subconjunto del dominio de f, C ⊆ A, y cuyas imágenes coinciden en este subconjunto:
se dice entonces que g es la restricción de f al subconjunto C, y que f es unaextensión de g.
|
La restricción de una función f: A → B a un subconjunto C ⊆ A se denota por f|C.
Representación de funciones
Las funciones se pueden presentar de distintas maneras:
- usando una relación matemática descrita mediante una expresión matemática: ecuaciones de la forma
 . Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama el dominio natural, de la función.
. Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama el dominio natural, de la función.
- Ejemplo: y=x+2. Dominio natural es todos los reales.
- Ejemplo: "Para todo x, número entero, y vale x más dos unidades".
- Como tabulación: tabla que permite representar algunos valores discretos de la función.
- Ejemplo:

- Ejemplo: A={(-2, 0),(-1, 1),(0, 2),(1, 3),... (x, x+2)}
- Ejemplo:
| 5 | | | | | | X |
| 4 | | | | | X | |
| 3 | | | | X | | |
| 2 | | | X | | | |
| 1 | | X | | | | |
| 0 | X | | | | | |
| y / x | -2 | -1 | 0 | 1 | 2 | 3 |
Definición formal. Generalizaciones
Las funciones pueden definirse en términos de otros objetos matemáticos, como los conjuntos y los pares ordenados. En particular, una función es un caso particular de relación binaria, luego su esta definición está basada en la que se adopte para las relaciones. En el enfoque «extensivo» se identifica una función con su gráfica:
Una función es un conjunto f de pares ordenados tal que no contiene dos pares distintos con la misma primera componente:
El dominio (la imagen) de la función es entonces el conjunto de primeras (segundas) componentes:
|
En la definición extensiva no aparece el concepto de codominio como conjunto potencial donde está contenido el recorrido. En algunas áreas de las matemáticas es importante preservar esta distinción, y por tanto se usa una definición distinta:8
Una función es una terna de conjuntos f = (A, B, G(f)), el dominio, elcodominio y el grafo de f, tales que:
- G(f) ⊂ A × B
- Todo elemento del dominio tiene imagen: para cada a ∈ A, existe unb ∈ B tal que (a, b) ∈ G(f)
- Esta imagen es única: si (a, b), (a, c) ∈ G(f), entonces b = c.
|
Con esta definición, dos funciones con el mismo grafo son distintas si su codominio no coincide. También se habla en ocasiones defunciones parciales, para las que no necesariamente cada elemento del dominio posee una imagen, en contraste con las funciones como se han definido antes, que se denominan totales. A las funciones parciales también se las llama correspondencias o relacionesunívocas.9
Inyectivo, sobreyectivo y biyectivo
"Inyectivo, sobreyectivo y biyectivo" te dan información sobre el comportamiento de una función.
Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B":
"Injectivo" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").
"Sobreyectivo" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno).
"Biyectivo" significa inyectivo y sobreyectivo a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.
Definiciones formales
Inyectivo
Una función f es inyectiva si, cuando f(x) = f(y), x = y.
Ejemplo: f(x) = x2 del conjunto de los números naturales  a
a  es una función inyectiva.
es una función inyectiva.
(Pero f(x) = x2 no es inyectiva cuando es desde el conjunto de enteros 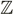 (esto incluye números negativos) porque tienes por ejemplo
(esto incluye números negativos) porque tienes por ejemplo
Nota: inyectiva también se llama "uno a uno", pero esto se confunde porque suena un poco como si fuera biyectiva.
Sobreyectivo (o también "epiyectivo")
Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.
Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.
Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.
al de los números pares no negativos es sobreyectiva.
Sin embargo, f(x) = 2x del conjunto de los números naturales  a
a  no es sobreyectiva, porque, por ejemplo, ningún elemento de
no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.
va al 3 por esta función.
Biyectiva
Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y
Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.
Ejemplo: La función f(x) = x2 del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.
(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo
 está definido por:2
está definido por:2 está definido por:2
está definido por:2 es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real. es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
es siempre positivo o cero, pero nunca negativo. En general, el valor absoluto de la diferencia de dos números reales es la distancia entre ellos. De hecho, el concepto de función distancia o métrica en matemáticas se puede ver como una generalización del valor absoluto de la diferencia, a la distancia a lo largo de la recta numérica real.
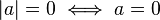



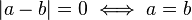
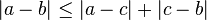


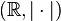 es un espacio de Banach.[cita requerida]
es un espacio de Banach.[cita requerida]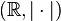 es un espacio de Banach.[cita requerida]
es un espacio de Banach.[cita requerida]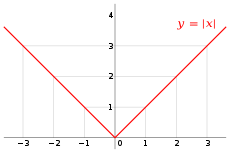


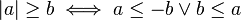




 es la distancia
es la distancia  desde
desde  tienen el mismo valor absoluto.
tienen el mismo valor absoluto.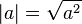

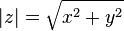




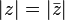
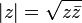






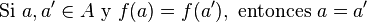




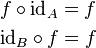




 . Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama el dominio natural, de la función.
. Cuando la relación es funcional, es decir satisface la segunda condición de la definición de función, se puede definir una función que se dice definida por la relación, A menos que se indique lo contrario, se supone en tales casos que el dominio es el mayor posible (respecto a inclusión) y que el codominio son todos los Reales. El dominio seleccionado se llama el dominio natural, de la función.